検証付きカバレッジ検査器

この記事は証明支援系 Advent Calendar 2025の18日目の記事です．

去年の春頃から少しずつパターンマッチのカバレッジ検査アルゴリズムの形式化を進めていて，それがある程度完成しました． この記事では，そのアルゴリズムや形式化について紹介したいと思います¹．

目次

• 背景
• $\mathcal{U}_\mathrm{rec}$ の概要
  • $\mathcal{U}_\mathrm{rec}$ の扱う体系
  • パターンの有用性
  • $\mathcal{U}_\mathrm{rec}$ の動作原理
    • $\overrightarrow{p}$ が空のベクタの場合
    • $\overrightarrow{p}$ の先頭がOrパターンの場合
    • $\overrightarrow{p}$ の先頭がコンストラクタパターンの場合
    • $\overrightarrow{p}$ の先頭がワイルドカードパターンの場合
• 形式化のハイライト
  • 正当性証明
  • 有用性の拡張
  • 停止性証明
  • agda2hsによるHaskellへの変換
• おわりに

背景

パターンマッチのカバレッジ検査は，パターンが網羅性と非冗長性の二つの嬉しい性質を満たしているかを検査する静的解析です．

• 網羅性: どんな値に対しても何らかのパターンにマッチすること
• 非冗長性: 実行が辿り着かないパターンがないこと

以下の例を見てみましょう．このOCamlプログラムでは単純なアクセス制御のための関数allowedをパターンマッチを用いて実装しています．

type role = Staff | Manager | Admin
type action = View | Edit | Approve | Delete

let allowed role action =
  match role, action with
  | _,                 View    -> true
  | (Manager | Staff), Delete  -> false
  | manager,           Approve -> true
  | Staff,             Approve -> false

このパターンは網羅的でしょうか？ いいえ，例えばStaff, Editのパターンを考慮し忘れています． このままでは，allowed Staff Editを評価した際に実行時例外が発生してしまいます．

では非冗長性はどうでしょうか？これも満たしません．三つ目のケースの role 側がManagerではなくmanagerという変数パターンになっています．したがってStaff, Approveの場合も三つ目のケースにマッチし，結果として四つ目のケースには辿り着きません．冗長なパターンがある時，それはプログラマが考えていたものとは異なる，予想外の場合分けとなっている可能性があります．

この例から分かるように，プログラムの安全性や予測可能性を高める上で，カバレッジ検査は重要な解析となっています．

カバレッジ検査のためのアルゴリズムは様々なものが考案されています．

• $\mathcal{U}_\mathrm{rec}$²
  • Rustのカバレッジ検査アルゴリズムの基礎になっている
  • 昔はOCamlコンパイラにも実装されていた
  • 単純なパターンしか扱わないが十分実用的である（大体のプログラムは単純なパターンで書けるため）
• Lower your guards³
  • Haskellのカバレッジ検査アルゴリズムの基礎になっている
  • 複雑なパターンも扱う（GADTs, View Patterns, Pattern Synonyms, Strictness, …）
• …

これらのアルゴリズムには紙とペンによる正当性の証明もついています．ありがたいですね．

しかし，アルゴリズムの実装はどうでしょうか？いくら紙とペンによる正当性の証明があったとしても，実装に間違いがあった場合，不適切なエラーを出したり，バグを見逃したりしてしまいます． カバレッジ検査は重要な検査ですから，実装まで含めて正しいことが検証されたカバレッジ検査器が欲しくなるわけです． 調査してみると，検証付きコンパイラを含めて探してみても，そのようなものはほとんど見つかりません⁴． そこで，自分がよく使っている証明支援系であるAgdaを用いて，カバレッジ検査アルゴリズムを形式化し検証付き実装を得ることにしました．

実装するアルゴリズムとしては $\mathcal{U}_\mathrm{rec}$ を選びました． $\mathcal{U}_\mathrm{rec}$ は比較的単純なので，証明支援系での形式化も実現しやすいと考えました．今後，より複雑な，あるいは効率的なアルゴリズムを形式化する際の基盤にもなりそうです．

$\mathcal{U}_\mathrm{rec}$ の概要

$\mathcal{U}_\mathrm{rec}$ の扱う体系

上述の通り，$\mathcal{U}_\mathrm{rec}$ は比較的単純な体系を扱います． 具体的には，値として代数的データ型のもののみを考え，パターンとしてはワイルドカードパターン，コンストラクタパターン，Orパターンの三種類だけを考えます． カバレッジ検査の際は，変数パターンはワイルドカードパターンとして扱えばいいです． $c$ から始まるものをコンストラクタ，$u, v, w$ から始まるものを値とします． また，$p, q, r$ から始まるものをパターンとします．

$$\begin{array}{rcl} u , v, w & \Coloneqq & c(v_1, \cdots, v_n) \\ p, q, r & \Coloneqq & \_ \\ & | & c(p_1, \cdots, p_n) \\ & | & (p \mid q) \\ \end{array}$$

値ベクタ $(v_1, \cdots, v_n)$ とパターンベクタ $(p_1, \cdots, p_n)$ をそれぞれ $\overrightarrow{v}$ や $\overrightarrow{p}$ のように書き，パターン行列（パターンベクタが並んだもの）を $P$ と書くことにします．パターン行列の各行が match 式の各ケースを表しています．

マッチすることを表す二項関係 $\preceq$ も導入しておきます⁵． （単一の）値がパターンにマッチする関係は以下のように標準的に定義されます．

$$\begin{array}{rclcl} v & \preceq & \_ \\ c(v_1, \cdots, v_n) & \preceq & c(p_1, \cdots, p_n) & \iff & (v_1, \cdots, v_n) \preceq (p_1, \cdots, p_n) \\ v & \preceq & (p \mid q) & \iff & v \preceq p\ \ \text{or}\ \ v \preceq q \end{array}$$

値ベクタがパターンベクタにマッチするのは，対応する要素がそれぞれマッチする時です． 特に，長さが0の値ベクタは長さ0のパターンベクタにマッチします．

$$(v_1, \cdots, v_n) \preceq (p_1, \cdots, p_n) \iff \forall\ i \in \{1, \cdots, n\},\ v_i \preceq p_i$$

さらに，値ベクタがパターン行列のいずれかの行にマッチすることを，値ベクタとパターン行列の間のマッチ関係として定義します．

$$\overrightarrow{v} \preceq P \iff \text{there exists a row } P_i \text{ in } P \text{ such that } \overrightarrow{v} \preceq P_i$$

明示されていませんが，値やパターンには型がついていて，$\preceq$ は同じ型の値とパターンに対してのみ定義されます．

例を見てみましょう．以下のリストのようなデータ型を考えます．

type mylist = Nil | One of unit | Cons of unit * mylist

そして，以下のパターン行列や値ベクタを考えます．

$$\begin{array}{c} P = \begin{pmatrix} \texttt{Nil} & \texttt{\_} \\ \texttt{\_} & \texttt{Nil} \end{pmatrix}\quad Q = \begin{pmatrix} \texttt{Nil} & \texttt{\_} \\ \texttt{\_} & \texttt{Nil} \\ \texttt{One(\_)} & \texttt{\_} \\ \texttt{\_} & \texttt{One(\_)} \\ \texttt{Cons(\_, \_)} & \texttt{\_} \\ \texttt{\_} & \texttt{Cons(\_, \_)} \end{pmatrix} \\ \\ \overrightarrow{u} = \begin{pmatrix} \texttt{Nil} & \texttt{Nil} \end{pmatrix}\quad \overrightarrow{v} = \begin{pmatrix} \texttt{One(Nil)} & \texttt{Nil} \end{pmatrix}\quad \overrightarrow{w} = \begin{pmatrix} \texttt{One(Nil)} & \texttt{One(Nil)} \end{pmatrix} \end{array}$$

この時，$\overrightarrow{u} \preceq P$ かつ $\overrightarrow{v} \preceq P$ です． それぞれ $P$ の第1行と第2行にマッチするからです． 一方で $\overrightarrow{w} \npreceq P$ です． また，$\overrightarrow{u}, \overrightarrow{v}, \overrightarrow{w} \preceq Q$ であることもわかります．

パターンの有用性

実は $\mathcal{U}_\mathrm{rec}$ は網羅性でも非冗長性でもなく有用性と呼ばれる性質を検査するアルゴリズムです．有用性の定義は以下のようになっています．

先ほどの例を引き続き用いて，有用性の例を見てみましょう．$P$ に対して $\overrightarrow{p} = (\texttt{\_}\ \ \texttt{\_})$ （ワイルドカードパターンのベクタ）は有用です．なぜなら，先ほどの $\overrightarrow{w} = (\texttt{One(Nil)}\ \ \texttt{One(Nil)})$ が証拠となるから（$\overrightarrow{w} \npreceq P$ かつ $\overrightarrow{w} \preceq \overrightarrow{p}$ が成り立つから）です． また，$Q$ の 第1~5行目 がなす小行列に対して，$Q$ の第6行目は有用でないことも確かめられます．

では，なぜ有用性を考えるのでしょうか？ 網羅性と非冗長性のどちらもが有用性を使って言い換えられるからです！

先ほどの有用性に関する二つの例は，それぞれ $P$ が網羅的でないことと $Q$ の第6行目が冗長であることを示していました．

この同値を利用することで，$\mathcal{U}_\mathrm{rec}$ さえあれば，それをもとに網羅性/非冗長性検査アルゴリズムを実装することができるのです．

$\mathcal{U}_\mathrm{rec}$ の動作原理

では，$\mathcal{U}_\mathrm{rec}$ を詳しく見ていきましょう．$\mathcal{U}_\mathrm{rec}$ の仕様は以下です．

• 入力: パターン行列 $P$ とパターンベクタ $\overrightarrow{p}$
• 出力: 真偽値
• 仕様:
  • $P$ と $\overrightarrow{p}$ の対応する列の型が一致していなければならない
  • $\overrightarrow{p}$ が $P$ に対して有用な時に限り真を返す ( $\mathcal{U}_\mathrm{rec}(P, \overrightarrow{p}) = \mathrm{True} \iff \mathcal{U}(P, \overrightarrow{p})$ )

$\mathcal{U}_\mathrm{rec}$ は有用性の証拠となる値ベクタを探索するような動作をします． $\overrightarrow{p}$ がどのようなパターンベクタであるかで場合分けしていき，有用性の証拠となる値ベクタを絞っていきます． それに応じて，$P$ の行のうち，証拠の値ベクタにマッチしないことが確定した行を除外することで，問題を小さくします．あとはこの部分問題を再帰的に解けば良いという算段です．

$\overrightarrow{p}$ が空のベクタの場合

再帰のベースケースであり，最も単純な有用性問題を解くステップです．$P$ は長さ0のパターンベクタが並んだ0列のパターン行列になっています． 空のパターンベクタには空の値ベクタがマッチすることを思い出すと，$P$ が空行列(0行0列)であるかどうかを結果として返せば良いことがわかります． $P$ が空行列である場合，空の値ベクタが有用性の証拠となるからです． 逆に $P$ が空行列でない場合，$() \preceq P$ なので $\overrightarrow{p}$ は有用でないと結論づけられます．

$$\mathcal{U}_\mathrm{rec}(P, \begin{pmatrix} \end{pmatrix}) = \begin{cases} \mathrm{True} & \text{if } P \text{ has no rows} \\ \mathrm{False} & \text{otherwise} \end{cases}$$

$\overrightarrow{p}$ の先頭がOrパターンの場合

左右のパターンのどちらかを選んだ場合を再帰的に解き，その論理和を取れば良いです．

$$\begin{align*} &\mathcal{U}_\mathrm{rec}( P, \begin{pmatrix} (p_l \mid p_r) & p_2 & \cdots & p_n \end{pmatrix} ) = \\ &\quad\quad \mathcal{U}_\mathrm{rec}( P, \begin{pmatrix} p_l & p_2 & \cdots & p_n \end{pmatrix} ) \lor \mathcal{U}_\mathrm{rec}( P, \begin{pmatrix} p_r & p_2 & \cdots & p_n \end{pmatrix} ) \end{align*}$$

$\overrightarrow{p}$ の先頭がコンストラクタパターンの場合

$\overrightarrow{p}$ の先頭が $c(r_1, \cdots, r_m)$ である場合，証拠となる値ベクタ $\overrightarrow{v}$ の先頭も $c(v_1, \cdots, v_m)$ のようになっている必要があります． したがって，$P$ の行のうち，先頭のパターンが $c'(\ \cdots)$ ($c'$ は $c$ と異なる) である行は除外できます． この除外処理（特殊化と呼ばれる操作）を行う関数を $\mathcal{S}$ とすれば，$\mathcal{U}_\mathrm{rec}$ は以下のように定義できます． コンストラクタパターンの中にネストしているパターンは展開されて $\overrightarrow{p}$ の頭にくっつけられます．

$$\begin{align*} &\mathcal{U}_\mathrm{rec}( P, \begin{pmatrix} c(r_1, \cdots, r_m) & p_2 & \cdots & p_n \end{pmatrix} ) = \\ &\quad\quad \mathcal{U}_\mathrm{rec}( \mathcal{S}(c, P), \begin{pmatrix} r_1 & \cdots & r_m & p_2 & \cdots & p_n \end{pmatrix} ) \end{align*}$$

$\mathcal{S}$ の定義は以下のようになります． 行の先頭にOrパターンが現れた場合は，Orパターンを展開して二つの行に分けます． また，ワイルドカードパターンは，コンストラクタ $c$ の引数の個数分だけのワイルドカードパターンに展開します．

$$\begin{array}{c} \mathcal{S}(c, \begin{pmatrix} \end{pmatrix}) = \begin{pmatrix} \end{pmatrix} \\ \mathcal{S}\left(c, \left(\begin{array}{c} \begin{matrix} (p_l \mid p_r) & p_2 & \cdots & p_n \end{matrix} \\ P \end{array}\right)\right) = \mathcal{S}\left(c, \begin{pmatrix} \begin{matrix} p_l & p_2 & \cdots & p_n \end{matrix} \\ \begin{matrix} p_r & p_2 & \cdots & p_n \end{matrix} \\ P \end{pmatrix} \right) \\ \mathcal{S}\left(c, \left(\begin{array}{c} \begin{matrix} c'(r_1, \cdots, r_m) & p_2 & \cdots & p_n \end{matrix} \\ P \end{array}\right)\right) = \begin{cases} \begin{pmatrix} \begin{matrix} r_1 & \cdots & r_m & p_2 & \cdots & p_n \end{matrix} \\ \mathcal{S}(c, P) \end{pmatrix} & \text{if } c = c' \\ \mathcal{S}(c, P) & \text{otherwise} \end{cases} \\ \mathcal{S}\left(c, \left(\begin{array}{c} \begin{matrix} \_ & p_2 & \cdots & p_n \end{matrix} \\ P \end{array}\right)\right) = \begin{pmatrix} \begin{matrix} \_ & \cdots & \_ & p_2 & \cdots & p_n \end{matrix} \\ \mathcal{S}(c, P) \end{pmatrix} \end{array}$$

$\overrightarrow{p}$ の先頭がワイルドカードパターンの場合

この場合では，先頭がコンストラクタパターンの場合とは違い，証拠となる値ベクタ $\overrightarrow{v}$ の先頭のコンストラクタが何であるかが $\overrightarrow{p}$ からは決まりません． そのため，基本的には，あり得るコンストラクタで特殊化した問題を解いてその論理和をとる，総当たりの手法を用いる必要があります．

$$\begin{align*} &\mathcal{U}_\mathrm{rec}( P, \begin{pmatrix} \_ & p_2 & \cdots & p_n \end{pmatrix} ) = \\ &\quad\quad \bigvee_{c_k : \text{ Constructor}} \mathcal{U}_\mathrm{rec}( \mathcal{S}(c_k, P), \begin{pmatrix} \_ & \cdots & \_ & p_2 & \cdots & p_n \end{pmatrix} ) \end{align*}$$

しかし，$P$ の情報を使うことで総当たりを避けてより効率的に解くことができる場合があります． 例をとって考えて見ましょう．$P$ と $\overrightarrow{p}$ が以下の場合を考えます．

$$\begin{align*} P = \begin{pmatrix} \texttt{Nil} & \texttt{\_} \\ \texttt{One(\_)} & \texttt{\_} \\ \texttt{\_} & \texttt{Nil} \\ \texttt{\_} & \texttt{One(\_)} \end{pmatrix} && \overrightarrow{p} = \begin{pmatrix} \_ & \texttt{Cons(\_,\_)} \end{pmatrix} \end{align*}$$

$P$ の1列目に着目すると，mylist 型のコンストラクタのうち Nil と One はありますが，Cons はありません． ここで，$\overrightarrow{v}$ の先頭のコンストラクタを Cons としてみましょう． すると，その値ベクタは P の行のうち先頭がワイルドカードパターンのもののみ（3,4行目）にしかマッチしないはずです．それらの行にだけ着目すると以下のようになります．

$$\begin{align*} P = \begin{pmatrix} \texttt{\_} & \texttt{Nil} \\ \texttt{\_} & \texttt{One(\_)} \end{pmatrix} && \overrightarrow{p} = \begin{pmatrix} \_ & \texttt{Cons(\_,\_)} \end{pmatrix} \end{align*}$$

$P$ と $\overrightarrow{p}$ の1列目が全てワイルドカードパターンになりました． 1列目のパターンが全て同じなので，$\overrightarrow{p}$ の $P$ に対する有用性は，2列目だけから決まりますね． あとは，以下の部分問題を解けば良いです．

$$\begin{align*} P = \begin{pmatrix} \texttt{Nil} \\ \texttt{One(\_)} \end{pmatrix} && \overrightarrow{p} = \begin{pmatrix} \texttt{Cons(\_,\_)} \end{pmatrix} \end{align*}$$

このように，$P$ の1列目に現れないコンストラクタ $c$ があった場合，$\overrightarrow{v}$ の先頭を $c(\text{\footnotesize{適当な値ベクタ}})$ としてあげれば，総当たりせずに効率的に問題を小さくできるのです⁶．

以上をまとめると，$\overrightarrow{p}$ の先頭がワイルドカードパターンの場合の $\mathcal{U}_\mathrm{rec}$ は，以下のように定義できます．

$$\begin{align*} &\mathcal{U}_\mathrm{rec}( P, \begin{pmatrix} \_ & p_2 & \cdots & p_n \end{pmatrix} ) = \\ &\quad\quad \begin{cases} \mathcal{U}_\mathrm{rec}( \mathcal{D}(P), \begin{pmatrix} p_2 & \cdots & p_n \end{pmatrix} ) & \text{if } \Sigma \text{ is incomplete} \\ \bigvee_{c_k} \mathcal{U}_\mathrm{rec}( \mathcal{S}(c_k, P), \begin{pmatrix} \_ & \cdots & \_ & p_2 & \cdots & p_n \end{pmatrix} ) & \text{otherwise} \end{cases} \end{align*}$$

ここで，$\Sigma$ は $P$ の1列目に現れるコンストラクタの集合です． また，$\mathcal{D}$ は先頭がワイルドカードパターンの行の2列目以降のみを取り出すような関数で，以下のように定義されます． $\mathcal{S}$ と同様に，先頭がOrパターンの場合はOrパターンを展開して二つの行に分けます．

$$\begin{array}{c} \mathcal{D}(\begin{pmatrix} \end{pmatrix}) = \begin{pmatrix} \end{pmatrix} \\ \mathcal{D}\left(\left(\begin{array}{c} \begin{matrix} (p_l \mid p_r) & p_2 & \cdots & p_n \end{matrix} \\ P \end{array}\right)\right) = \mathcal{D}\left(\begin{pmatrix} \begin{matrix} p_l & p_2 & \cdots & p_n \end{matrix} \\ \begin{matrix} p_r & p_2 & \cdots & p_n \end{matrix} \\ P \end{pmatrix} \right) \\ \mathcal{D}\left(\left(\begin{array}{c} \begin{matrix} c(r_1, \cdots, r_m) & p_2 & \cdots & p_n \end{matrix} \\ P \end{array}\right)\right) = \mathcal{D}(P) \\ \mathcal{D}\left(\left(\begin{array}{c} \begin{matrix} \_ & p_2 & \cdots & p_n \end{matrix} \\ P \end{array}\right)\right) = \begin{pmatrix} \begin{matrix} p_2 & \cdots & p_n \end{matrix} \\ \mathcal{D}(P) \end{pmatrix} \end{array}$$

以上が $\mathcal{U}_\mathrm{rec}$ の動作原理です．

形式化のハイライト

では，いよいよ形式化について見ていきましょう． とはいえ，形式化でやることは動作原理のパートで説明したことを地道にAgdaに書き下すだけなので，この記事では重要な部分だけをいくつか紹介します．

正当性証明

形式化のメインとなる部分です． 今回，正当性証明はevidence-producingな $\mathcal{U}_\mathrm{rec}$ を実装することで行いました． オリジナルの $\mathcal{U}_\mathrm{rec}$ は有用性を表す真偽値だけを返す関数でしたが， 実際に実装したものは，有用性の証拠を明示的に計算して返すようになっています．

以下がその擬似コードです． Useful 型は有用性の定義をそのままAgdaに持ってきたようなレコード型です． 有用性の証拠 witness と，それが確かに証拠となっている証明 witness-does-not-match-P と witness-matches-ps を持っています． そして decUseful が $\mathcal{U}_\mathrm{rec}$ を実装した関数です． 返り値の型が Dec (Useful P ps) となっており，ps が P に対して有用ならその証拠を，そうでないなら証拠がないことの証明を返すようになっています．

record Useful (P : PatternMatrix) (ps : Patterns) : Type where
  field
    witness : Values
    witness-does-not-match-P : witness ⋠ P
    witness-matches-ps : witness ≼ ps

data Dec (A : Type) : Type where
  Yes : A → Dec A
  No : ¬ A → Dec A

decUseful : (P : PatternMatrix) (ps : Pattern) → Dec (Useful P ps)

このようにすることで，実装と正当性証明を同時に行なうことができ，Correct-by-Constructionな実装を得ることができます． さらに，decUsefulから得られる証拠は，カバレッジ検査のエラーメッセージをわかりやすくするのにも役立ちます． 網羅されていない部分がどれであるかを具体的に表示するのに使えるのです！

有用性の拡張

たった今，有用性の証拠をエラーメッセージ表示に活用できると言いました． しかしよく考えてみると，実際のコンパイラは，「網羅されていない値」ではなく「網羅されていないパターン」を表示してくれます．

例えば，以下のOCamlプログラムを考えます．

let foo (xs : mylist) (ys : mylist) : string =
  match xs, ys with
  | Nil, _   -> "nil-wildcard"
  | _  , Nil -> "wildcard-nil"

このプログラムに対し，OCamlコンパイラは以下のようなエラーメッセージを表示してくれます．

Warning 8: this pattern-matching is not exhaustive.
Here is an example of a case that is not matched:
((One _|Cons (_, _)), (One _|Cons (_, _)))

値よりもパターンを表示してくれた方が，情報量が多いので嬉しいですね． なので，decUseful も証拠となるパターンベクタ（の非空集合）を返すように，有用性の定義とアルゴリズムを拡張したいところです．

どのように有用性の定義を拡張すれば良いでしょうか？ 有用性のオリジナルの定義を思い返してみましょう．図にすると以下のようになります． $P$ と $\overrightarrow{p}$ のカバーする値ベクタの集合がそれぞれあります． そして，その差集合 $\overrightarrow{p} \setminus P$ の中の要素が，図中に点で表されている，有用性の証拠 $\overrightarrow{v}$ となります．

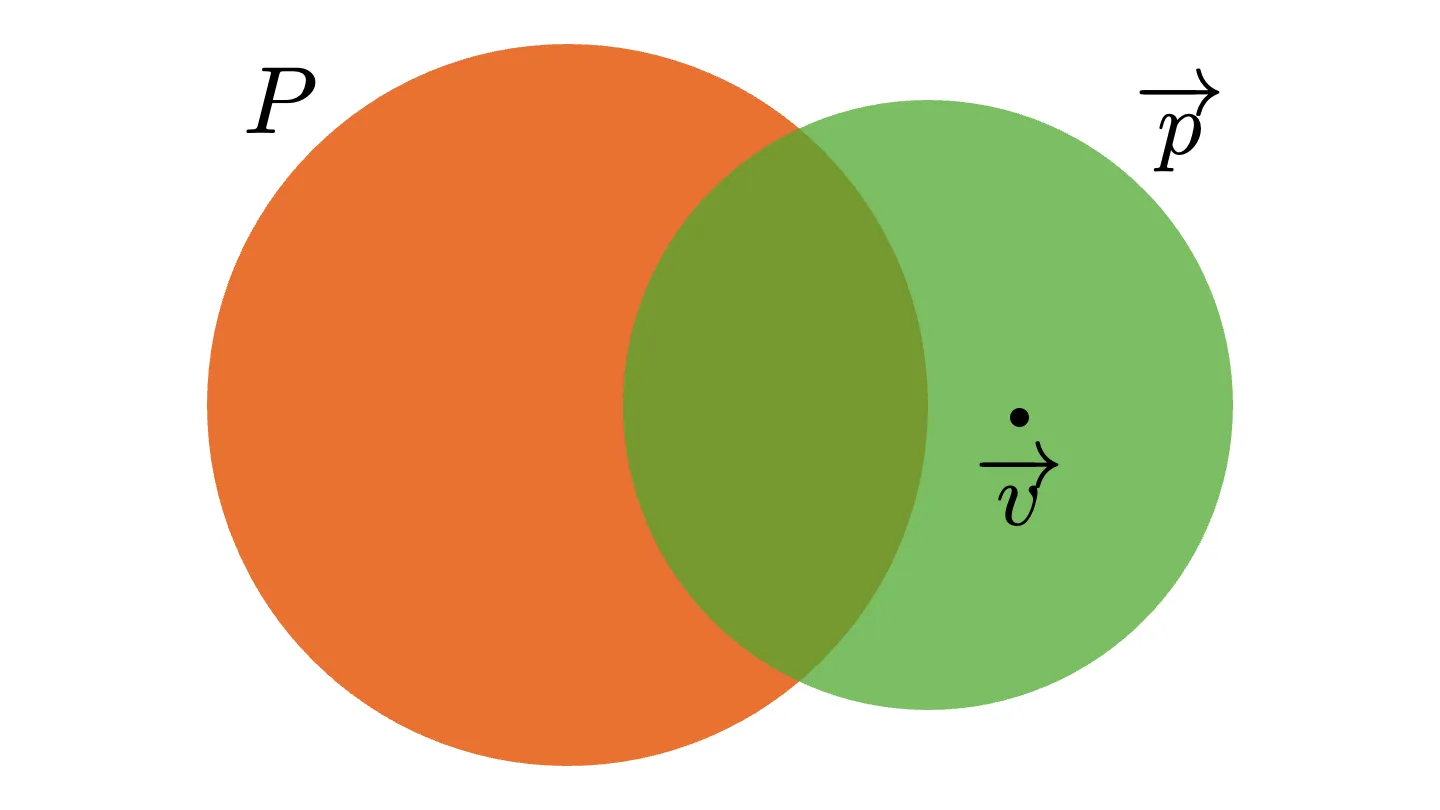
拡張した有用性の定義では，有用性の証拠をパターンベクタとしたかったのでした． そのためには，図中の $\overrightarrow{q}$ のように，証拠を点から集合へと膨らませば良さそうです． つまり，有用性の証拠を差集合の部分集合へと拡張します．

この直観を定式化すると以下のようになります．

「マッチしない」が「排他的である」に，「マッチする」が「包含される」に変わりました．

この拡張した有用性はきちんとオリジナルの有用性の一般化になっており，拡張した有用性からオリジナルの有用性を導くことができます．

では，この拡張した有用性を検査するためのアルゴリズムはどうなっているべきでしょうか？ 実は，元のアルゴリズムと大きく変える必要はありません． 変えるべきところと言えば，元のアルゴリズムで論理和をとっていた部分（Orパターンの場合とワイルドカードパターンで総当たりをする場合）だけです． 論理和をとる代わりに和集合をとることで，証拠となるパターンベクタ全てを返すようにします．

擬似コードは以下のようになります． Useful 型の定義が拡張されている他，decUseful の返り値の型が Dec (NonEmpty (Useful P ps)) となっており，有用性の証拠となるパターンベクタの非空リストを返すようになっています．

record Useful (P : PatternMatrix) (ps : Patterns) : Type where
  field
    witness : Patterns
    witness-disjoint-from-P : ∀ {vs} → vs ≼ witness → vs ≼ P → ⊥
    ps-subsumes-witness : ∀ {vs} → vs ≼ witness → vs ≼ ps

decUseful : (P : PatternMatrix) (ps : Pattern) → Dec (NonEmpty (Useful P ps))

decUseful の返す証拠が完全であること（$\overrightarrow{p} \setminus P$ を取り尽くしていること）は，まだ証明していないので，今後証明する予定です．

停止性証明

停止性も重要な性質です．コンパイラがカバレッジ検査で無限ループしまっては困るからです． しかし，元の論文では $\mathcal{U}_\mathrm{rec}$ の停止性の証明が与えられていませんでした．

$\mathcal{U}_\mathrm{rec}$ の停止性証明は結構トリッキーです．というのも，動作原理のパートで見たように，$\mathcal{U}_\mathrm{rec}$ が複雑な再帰構造を持つからです．構造的再帰ではないので整礎帰納法を使うことになりますが，それに用いる尺度を見つける上で以下の部分が困りものです．

1. $\mathcal{S}$ や $\mathcal{D}$ がOrパターンを展開する
2. $\mathcal{S}$ がワイルドカードパターンを複数のワイルドカードパターンに展開し得る

これらのせいで，単純なパターンの大きさは減らないどころか増えてしまうことまであります．最終的には，大まかに以下のようなアイデアで適切な尺度を見つけて，停止性を証明することができました！

1. パターンの大きさはOrパターンを全部展開してから数える⁷
2. ワイルドカードパターンを数えない
3. 2の結果としてサイズが狭義減少しなくなる場合が出てくるので，そのステップで減る別のサイズ（パターン行列の列数など）を組み合わせた辞書式順序を考える

agda2hsによるHaskellへの変換

今回のゴールは検証付きカバレッジ検査器を得ることなので，Agdaのコードを実行可能な形式に持っていけるようにしたいです． その方法として，今回はagda2hsを使うことにしました． agda2hsはAgdaのサブセットをなるべく元のコードに近いHaskellコードに変換するツールです．Agdaに付属しているHaskellへのコンパイラとは違い，人に読みやすいHaskellコードを生成することを目指しています．

agda2hsでは，Agdaのコードのどの部分をHaskellに変換するかを，erasureという機能を使って指定します．Agdaコード中で @0（または @erased）で注釈をつけた部分がHaskell側では消えているという具合です． 例えば，上の擬似コードで示した Useful 型に対して以下のように注釈をつけたとします． witness-disjoint-from-P と ps-subsumes-witness は証明のためだけの情報でありHaskell側では不要なので，消そうというわけです．

record Useful (@0 P : PatternMatrix) (@0 ps : Patterns) : Type where
  field
    witness : Patterns
    @0 witness-disjoint-from-P : ∀ {vs} → vs ≼ witness → vs ≼ P → ⊥
    @0 ps-subsumes-witness : ∀ {vs} → vs ≼ witness → vs ≼ ps

これをagda2hsで変換すると，以下のようなHaskellコードを得られます．

newtype Useful = Useful { witness :: Patterns }

このような調子で，形式化全体に頑張って @0 をつけてまわることで，直接Haskellで実装したものと大差ないコードを得られるようになります！

おわりに

この記事では，Agdaを使って検証付きカバレッジ検査器を実装した話をしました．

今後は，今回の形式化をベースとして，より複雑/効率的なアルゴリズムを形式化していきたいと思います． まずは，Rustで実装されている，網羅性と各節の非冗長性を一気に検査するように最適化されたバージョン⁸の形式化に取り組みたいです．

形式化したコード全体をGitHubで公開しています． haskellブランチにはagda2hsで生成したHaskellコードも載せています． さらに，HTMLに変換したコードもGitHub Pagesでホストしているので，実際の実装がどのようになっているか興味があれば見てみてください．

index

wasabi315.github.io

Footnotes

1. 去年のAdvent Calendarにこの記事を書くつもりだったのですが，停止性の証明につまってしまい，今年になってしまいました．実はこの形式化について論文も書いていて，今後出版される予定です．Pre-printはここで公開しています． ↩

2. Luc Maranget, Warnings for Pattern Matching. この論文はアルゴリズムをいくつか提案しており，$\mathcal{U}_\mathrm{rec}$ はその中の一番基本的なものです． ↩

3. Sebastian Graf, Simon Peyton Jones, and Ryan G. Scott, Lower your guards ↩

4. 自分の調べた限り，concurrent workであるJoshua M. Cohen, A Mechanized First-Order Theory of Algebraic Data Types with Pattern Matching以外には見つかりませんでした．そしてこの論文も同様に先行研究が見当たらないことを主張しています． ↩

5. 元論文とオペランドを逆にしています．こちらの順序の方が，集合の $\in$ と似ていて見やすいと思います． ↩

6. コンストラクタの引数の型に空の型 (Haskellの Void) が含まれていると，「適当な値ベクタ」が存在しなくなってしまいます．そこで，$\mathcal{U}_\mathrm{rec}$ は「全ての型に値が存在する」という仮定を置いています． ↩

7. 実際はOrパターンの数もサイズに含めます．展開して数えたサイズだけではOrパターンのステップでサイズが減らなくなるからです． ↩

8. 現状では，網羅性検査と各節に対しての非冗長性検査をそれぞれ行わなければならないので，節の数に比例した回数だけ $\mathcal{U}_\mathrm{rec}$ を呼び出すことになります． ↩